【算法学习笔记】棋盘覆盖问题演示程序

发表于 | 分类于 |

引子

棋盘覆盖问题采用的是分治策略。通过十字划分，将原问题转化为四个规模较小的棋盘覆盖问题。递归的使用这种分割，将问题最简化。

问题简述

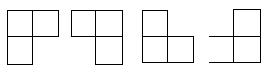
在一个 2^k 2^k个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ，有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何 2 个 L 型骨牌不得重叠覆盖。易知，在任何一个 2^k 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。

题解

用分治策略，可以设计解棋盘问题的一个简捷的算法。
当k>0时，将2^k 2^k棋盘分割为4个2^(k-1) 2^(k-1)子棋盘，如下图所示。

特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，我们可以用一个L型骨牌覆盖这3个较小的棋盘的汇合处，如下图所示，这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题化为4个较小规模的棋盘覆盖问题。递归的使用这种分割，直至棋盘简化为1x1棋盘。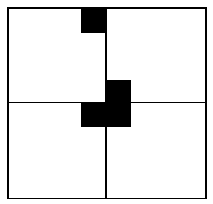

C++ Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<iostream>

using namespace std;

int tile=1;     //L型骨牌的编号(递增)
int board[100][100];    //棋盘
/*****************************************************
* 递归方式实现棋盘覆盖算法
* 输入参数：
* tr--当前棋盘左上角的行号
* tc--当前棋盘左上角的列号
* dr--当前特殊方格所在的行号
* dc--当前特殊方格所在的列号
* size：当前棋盘的:2^k
*****************************************************/
void chessBoard ( int tr, int tc, int dr, int dc, int size )
{
    if ( size==1 )    //棋盘方格大小为1,说明递归到最里层
        return;
    int t=tile++;     //每次递增1
    int s=size/2;    //棋盘中间的行、列号(相等的)
    //检查特殊方块是否在左上角子棋盘中
    if ( dr<tr+s && dc<tc+s )              //在
        chessBoard ( tr, tc, dr, dc, s );
    else         //不在，将该子棋盘右下角的方块视为特殊方块
    {
        board[tr+s-1][tc+s-1]=t;
        chessBoard ( tr, tc, tr+s-1, tc+s-1, s );
    }
    //检查特殊方块是否在右上角子棋盘中
    if ( dr<tr+s && dc>=tc+s )               //在
        chessBoard ( tr, tc+s, dr, dc, s );
    else          //不在，将该子棋盘左下角的方块视为特殊方块
    {
        board[tr+s-1][tc+s]=t;
        chessBoard ( tr, tc+s, tr+s-1, tc+s, s );
    }
    //检查特殊方块是否在左下角子棋盘中
    if ( dr>=tr+s && dc<tc+s )              //在
        chessBoard ( tr+s, tc, dr, dc, s );
    else            //不在，将该子棋盘右上角的方块视为特殊方块
    {
        board[tr+s][tc+s-1]=t;
        chessBoard ( tr+s, tc, tr+s, tc+s-1, s );
    }
    //检查特殊方块是否在右下角子棋盘中
    if ( dr>=tr+s && dc>=tc+s )                //在
        chessBoard ( tr+s, tc+s, dr, dc, s );
    else         //不在，将该子棋盘左上角的方块视为特殊方块
    {
        board[tr+s][tc+s]=t;
        chessBoard ( tr+s, tc+s, tr+s, tc+s, s );
    }
}

void main()
{
    int size;
    cout<<"输入棋盘的size(2^n): ";
    cin>>size;
    int x,y;
    cout<<"输入特殊方格位置坐标: ";
    cin>>x>>y;
    chessBoard ( 0,0,x,y,size );
    for ( int i=0; i<size; i++ )
    {
        for ( int j=0; j<size; j++ )
            cout<<board[i][j]<<"\t";
        cout<<endl;
    }
}

EGE演示程序

我自己用EGE做了一个图形化演示，但效果并不理想，代码核心内容如上，就不贴代码了。如图