1.Python命令行
在linux下输入python(windows下点击开始->程序->Python 2.3 ->IDLE(Python GUI)
在>>>提示符后输入print(‘Hello World!’)
Hello World!
2.Python小程序
用文本编辑器写一个.py结尾的文件,比如说helloWorld.py中写入print(“Hello World”) 在命令提示符中输入Python helloWorld.py,会在窗口中显示以下结果
Hello World!
3.Python脚本
下面将刚才的Python小程序改写成Python脚本
#!/usr/bin/env python
print("""Hello World!""")
更改helloWorld.py文件的权限
sudo chmod 755 helloWorld.py
输入./helloWorld.py即可之行该脚本,输入结果如下
Hello World!
知识点:
1.单引号、双引号、多引号的区别
*先说双引号与3个双引号的区别,双引号所表示的字符串通常要写成一行如果要写成多行,那么就要使用\ (“连行符”)
1 | s1 = "hello,world" # s2与s1是一样的。 |
如果你用3个双引号的话,就可以直接写了,如下:
1 | s3 = """hello, #s3实际上就是"hello,\nworld,\nhahaha.", “\n”是换行符。 |
如果你的字符串里\n很多,你又不想在字符串中用\n的话,那么就可以使用3个双引号。而且使用3个双引号还可以在字符串中增加注释,如下:
1 | s3 = """hello, #hoho, this is hello, 在3个双引号的字符串内可以有注释哦 |
单引号与双引号的作用是相同的。但是为什么要引入单引号和双引号呢?
举个例子:
当我用单引号来表示一个字符串时,如果要表示 Let’s go 这个字符串,必须这样:s4 = 'Let\'s go'注意没有,字符串中有一个’,而字符串又是用’来表示,所以这个时候就要使用转义符 \ (\,转义符应该知道吧), 如果你的字符串中有一大堆的转义符,看起来肯定不舒服python也很好的解决了这个问题。
如下:s5 = "Let's go"这时,我们看,python知道你是用 “ 来表示字符串,所以python就把字符串中的那个单引号 ‘ , 当成普通的字符处理了,是不是很简单?
对于双引号,也是一样的,下面举个例子s6 = 'I realy like "python"!'这就是单引号和双引号都可以表示字符串的原因了。
2.在Python 2.x中,print还可以是一个关键字,可写成print ‘Hello World!’,但这在3.x中行不通。
3.“#!/usr/bin/python”与”#!/usr/bin/env python”的区别(windows用户可以无视)
#!/usr/bin/python 是告诉操作系统执行这个脚本的时候,调用/usr/bin下的python解释器;相当于写死了Python的路径,如果Python的路径改变,脚本将无法执行。不推荐使用
#!/usr/bin/env python 这种用法是为了防止操作系统用户没有将python装在默认的/usr/bin路径里。当系统看到这一行的时候,首先会到env设置里查找python的安装路径,再调用对应路径下的解释器程序完成操作。
4.如何通过直接输入helloWorld.py而不是./helloWorld来执行脚本?(windows用户请无视)
在一般用户下输入PATH=$PATH:(注意后面的冒号)。 即可直接通过输入helloWorld.py执行脚本。
但是值得注意的是,千万不要用这种方法修改超级用户(一般是root)的PATH变量。这是一个安全网面 的漏洞,因为root用户管理员可能因此执行一个某个命令的伪装版本。
5.如何使你的程序在任何位置执行?
PATH=/home/userName/test:$PATH //将/home/userName/test加入PATH (注意中间的冒号! PATH必须大写!)
sudo cp helloWorld.py /home/userName/test/helloWorld
然后输入helloWorld即可直接之行脚本
6.Python的注释
1 | #单行注释 |
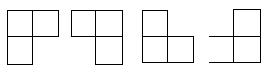
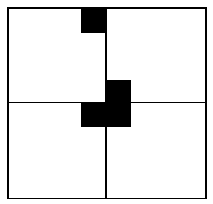
 在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个 2^k 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个 2^k 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。